Graphical Representation of Data

Graphical Representation of Data

Now that the data have been classified, the important characteristics of the distribution of the data are much clearer. However, a graphical representation will make the characteristics stand out even more. Incidentally, just by examining the tallies in we have a sort of graphic representation. Besides, many people prefer data to be presented in a graphic form rather than in a numerical form. In this article, we will discuss three types of graphs which are commonly used to present data such as that in the frequency distribution in.

• Histogram
• Frequency polygon
• Ogire

Histogram Graph

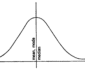
The graphical histogram is the most common type of graph for displaying classified data. A histogram is a bar graph with no space between bars. It is drawn on a pair of co-ordinate axes. With the unit of measurement for the observations being measured along the horizontal ants. The number or proportion of observations being measured along the vertical axis. The vertical scale or y-anis is usually taken to begin at zero. The horizontal scale or z-axis can begin at any convenient number. One simply selects any convenient point at which to begin the classes.

Explanation

The class boundaries are marked off on the horizontal axis. The difference in value between any two successive class boundaries is represented by the width of that class interval. A rectangle, the width of whose base equals the width of the class interval. And whose height is determined by the number of observations, is drawn for each class. Usually, if the class intervals are equal, the distances between the boundaries are drawn as equal. Each distance marked off on the horizontal axis may now be used as the base of a rectangle. The height of each rectangle will be determined by the class frequency.

The number of observations within that class is called frequency. An important property of a histogram is that the area of each rectangle is proportional to the number of observations in the corresponding class. In the infrequent situation where unequal class intervals are used. One needs to be careful that the areas of the rectangles are proportional to the number of observations in the classes.

Example

For example, suppose that for one reason or another we decide to combine the last three classes into a single class. The class interval of the class thus formed would be 75 units. The class frequency would be 8. Since the class interval is three times that of the other classes. If we made the height of the rectangle 8 units the area of the last rectangle would be three times as much as it should be. It should be clear that if the class interval of a particular class is three times that of the other classes.

Then,

the rectangle corresponding to it should be only one-third as tall as the rectangle corresponding to any other class which contains the same number of observations. Thus the rectangle corresponding to the wide class we are discussing should be  units high. As we have already seen, the division of the range of the observations into classes is entirely arbitrary, although some hints concerning good practice can be given. The classes must be described in such a way that there is no ambiguity about the class in which each observation should be placed. The number of classes can be as small as five or six for sample sizes of twenty-five or so. Eight or ten classes can conveniently be used for samples of about fifty observations.

For larger

samples from ten to twenty classes will, in general, be most satisfactory. The number of classes and the class interval should be chosen so that the range of the observations is cover deficiently, with not too much unnecessary room at the ends, and with about the same amount of ‘spare room below the smallest observation and above the largest one.

Frequency Polygon Graph

The frequency polygon, graphical is formed by placing a dot at the mid-point, i.e. the class mark, of the top of each rectangle of the histogram and connecting the dots. Dots can be placed over each class mark at the proper height, if the histogram is not drawn. Dots are usually placed on the horizontal axis one-half a class interval to the left of the lowest class and one- half a class interval to the right of the highest so that the polygon will be closed.

Ogire or Ogive Graphical

The graph of the cumulative frequency distribution is called an ogive. Many ogives have an appearance which is distinctly S-shaped. The ogive is drawn on a pair of perpendicular axes, just as the histogram and the frequency polygon are. With the horizontal axis representing the values of the observations and the vertical axis representing the number or proportion of observations.

Dots are placed opposite each of the numbers 450, 475, … 750, at whatever height is appropriate, to indicate how many observations are less than that value. For instance, the dot opposite 450 would be at a height of 1 unit and the dot opposite 600 would be at a height of 56. After all the dots have been located they are connected and the ogive is completed.