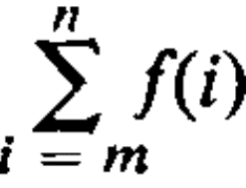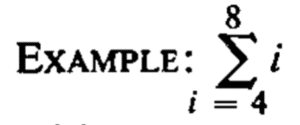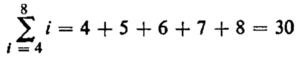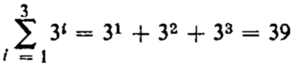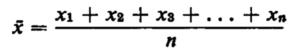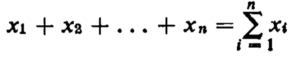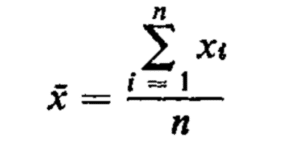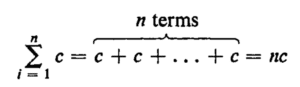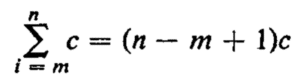Summation Notation – Definition – Example
Definition of summation notation
In statistics summation notation, we frequently need to indicate the sum of a large number of terms. It is convenient to have a shorthand notation for such an indicated sum. The standard mathematical symbol which denotes a sum is as follows.
However, the capital Greek letter ‘s’ (used because ‘s’ is the first letter of the word ‘sum’), called sigma, another name for summation notation. The most general appearance of an indicated sum using the sigma-notation is as follows.
Where the letter i is called the index of summation. m and n are called limits of summation and are integers with n greater than or equal to in (written symbolically as n ≥ m). And f(i) is some expression involving i—a function of i, to use mathematical terminology. In words, the above symbol means ‘in the expression f(i), replace i successively by m, by m + 1 …, and by n, and add the resulting terms.’Symbolically it is represented as follows.
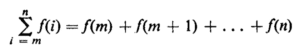
Equation of summation notation
Example
In above example, it means replace i successively by 4, 5, 6, 7, and 8 and add the resulting terms.
We have
Similarly,
and,
= 1 + 2 + 9
=12
Note: Recall that any non-zero number raised to the zero power is defined to be equal to 1. In particular, in the above example, 1° = 1.
Frequently in statistics we are interested in sums of observations or of quantities which are functions of the observations. For instance, we have previously defined the sample mean having formula as.
Therefore for the mean of summation notation, we can write the sum or X1 + X2 + … + Xn in an abbreviated fashion by using summation notation because
So, using summation notation, the definition of mean becomes
General Properties of Summation notation
Some general properties of the summations of various quantities are derived below. We will refer to these properties occasionally throughout the book, so you should become familiar with them. If the expression f(i) does not contain an i it is called a constant function, or more simply, a constant. So f(i) = 3,f(i) = 15a, and f(i) = c are examples of constant functions. By our rule, the symbol c means that in the expression f(i) = c we should replace i by 1, i by 2, and so on, until finally we replace i by n. Then we are to add the resulting terms.
When we replace i by 1 in the expression f(i) = c.
we get f(l) = c.
when we replace i by 2 we get f(2) = c and so on.
So we have
Stated verbally, when we sum a constant from i = 1 to i = n we get n times that constant. More generally it is represented as follows.